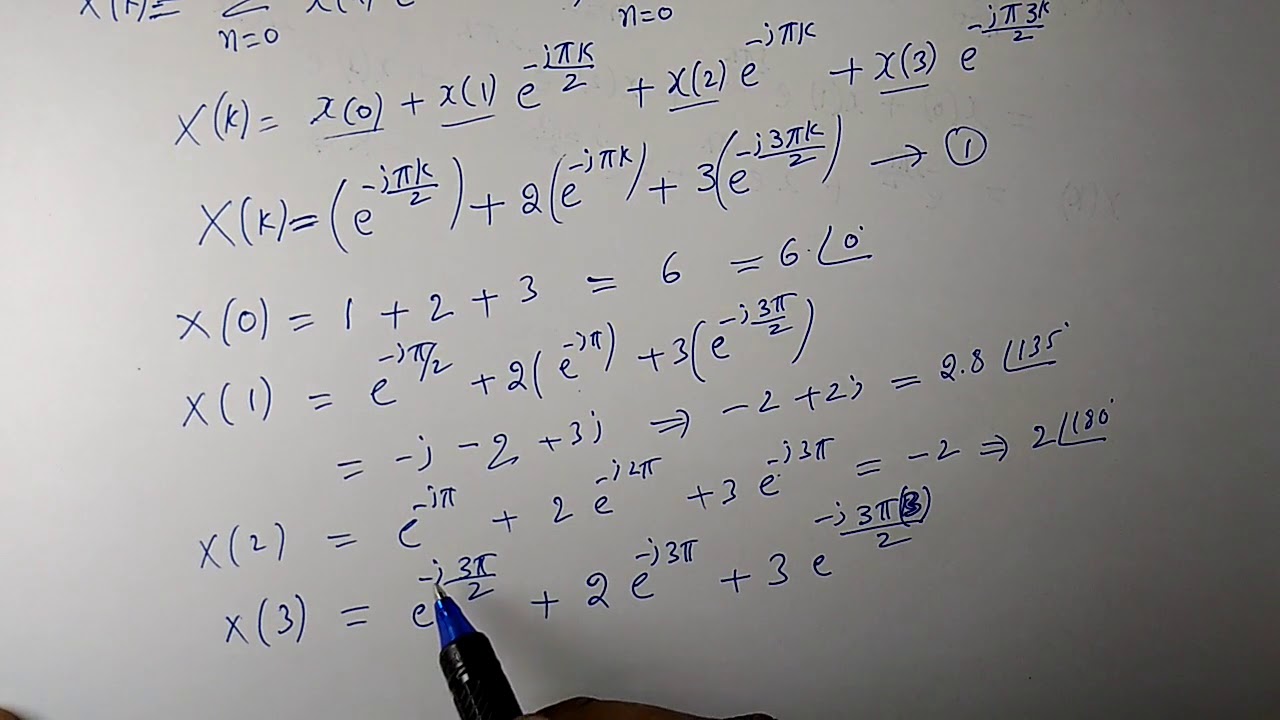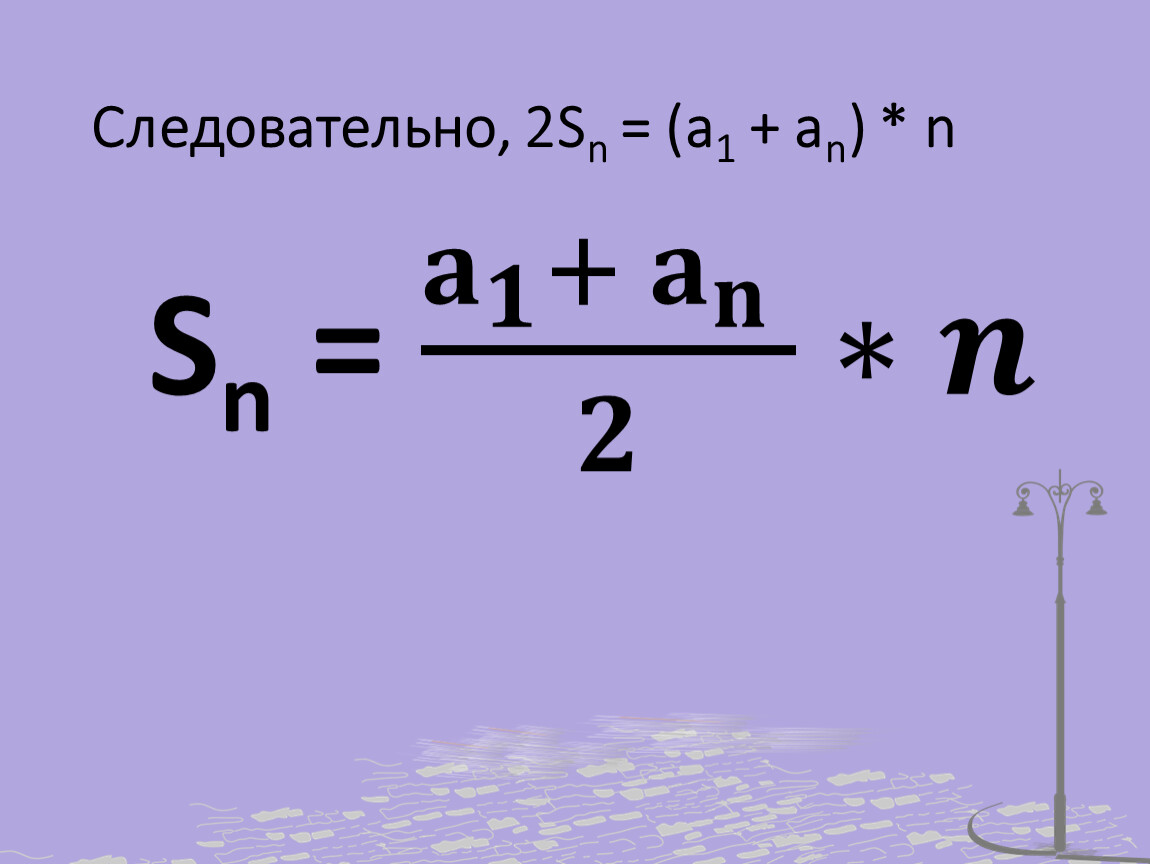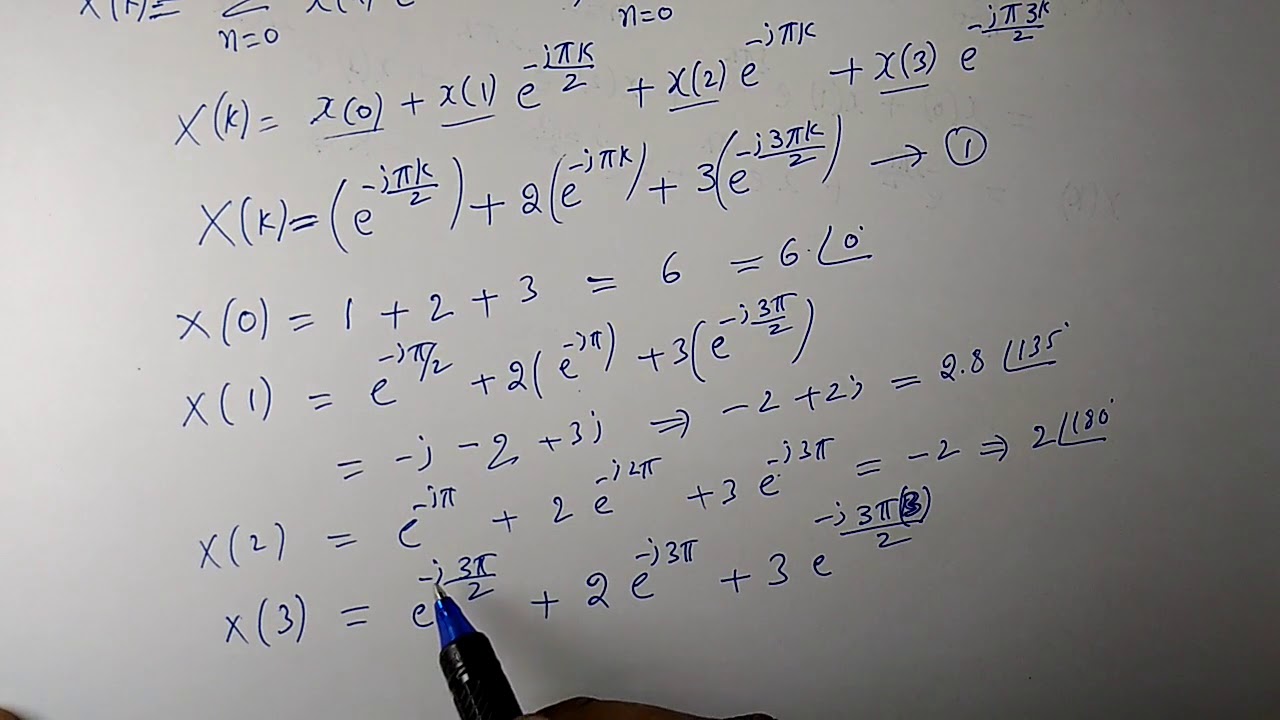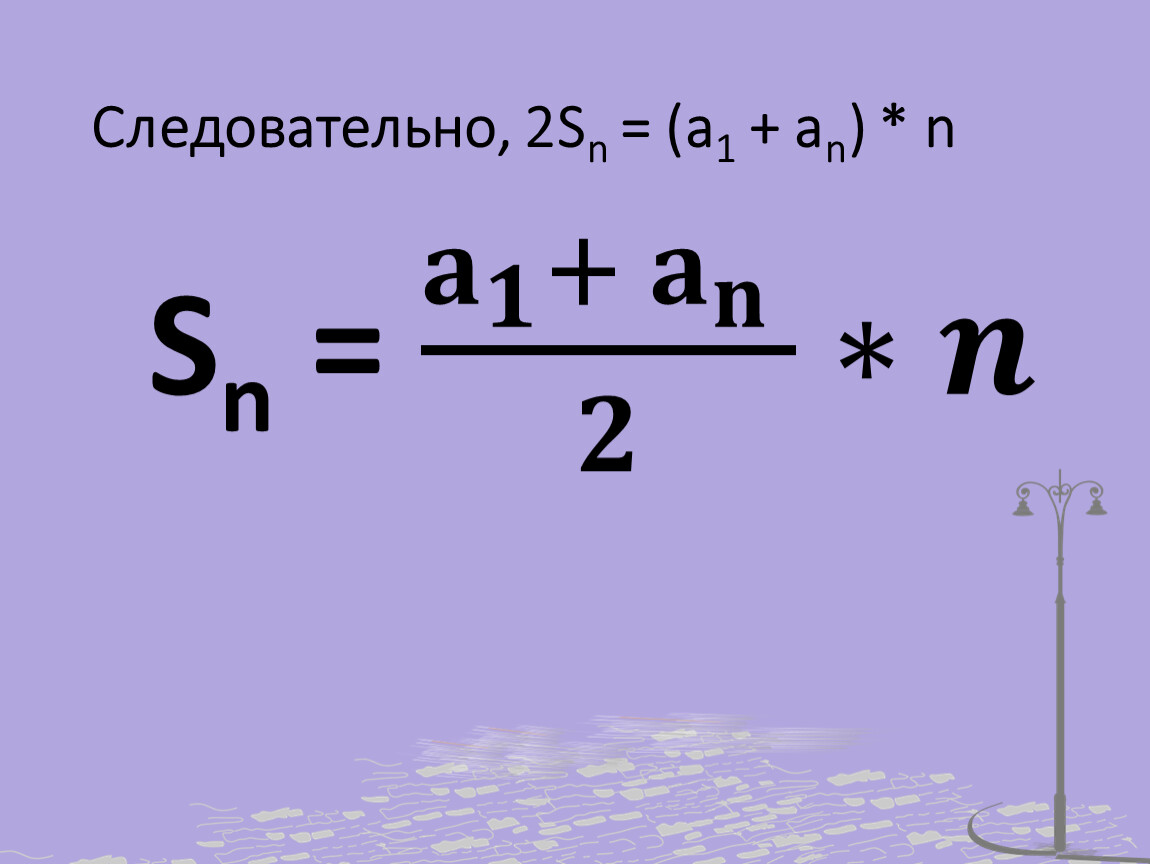Упростите выражения -9(3x-1/9)+(x+4/9). 1 2 2 2 n n n. (2n+1)(2n-1). Формула sn a1+an n/2. Discrete fourier transform samples.
|
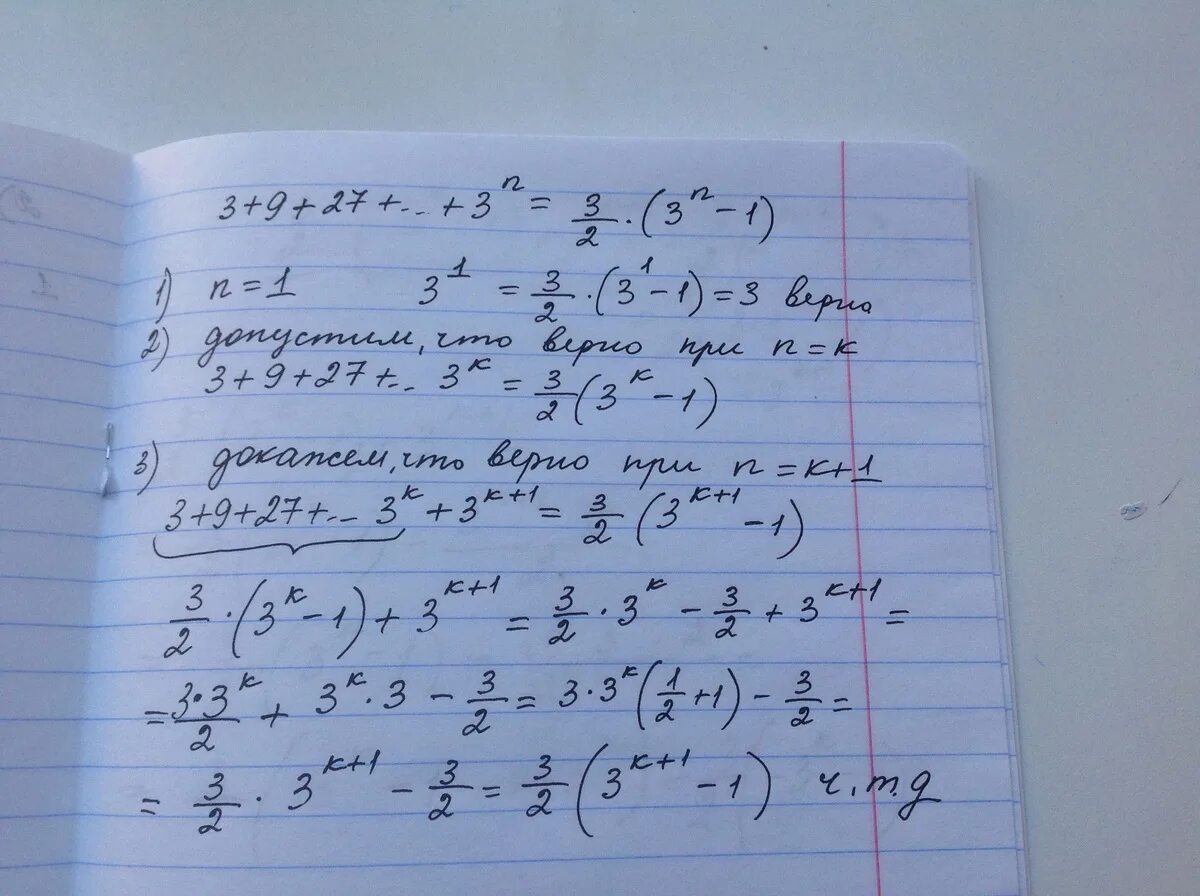2n 9 1 1 3. Упростите выражение n+3/2n+2 n+1/2n-2 3/n. (2n-1)/2^n. 2n 9 1 1 3. 2n 9 1 1 3.
|
(2n)! факториал 2n. Упростить выражение(n+2)!/ (n-2)! * (n+2). Упростить выражение n+3/2n+2-n+1/2n-2+3/n 2-1p. 2n 9 1 1 3. +1^3 =m.
|
4 9 2 7m 2 1 4 n -4. -1^6n - -1^2n + 3. (3n2 - 8n + 7) / (n - 2). 3m +4/9m2-4 + 3/4-6m. 3/х+2-5/х-3 -9/2.
|
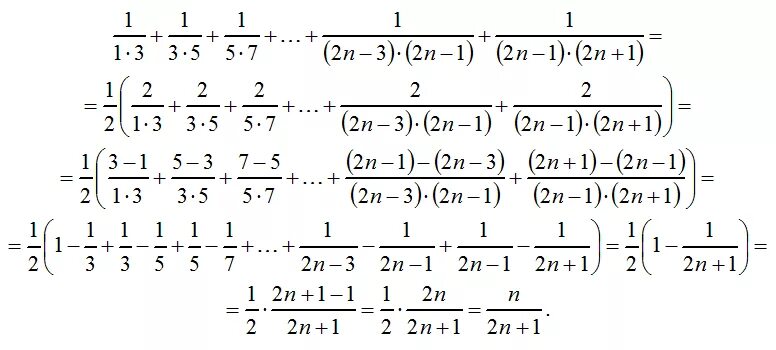Доказать математической индукцией 1/2 + 2/2^2. 2n 9 1 1 3. Сумма 1/1 + 1/2 + 1/3. Lim 4n^+3n-2 n=бесконечность х2n^-n+1. (2n-1)/2^n.
|
2n 9 1 1 3. Предел 1/n+1 1/n+2. 1^2+2^2+3^2+. 0001. 2n 9 1 1 3.
|
An = -5n/n+1, a=-5. Доказать, что 1 + 1/2 + 1/3. 1/2 + 3/2**2 +. Предел (n+1)^2/2n^2. 2n/3+n +9/n2-3n+9.
|
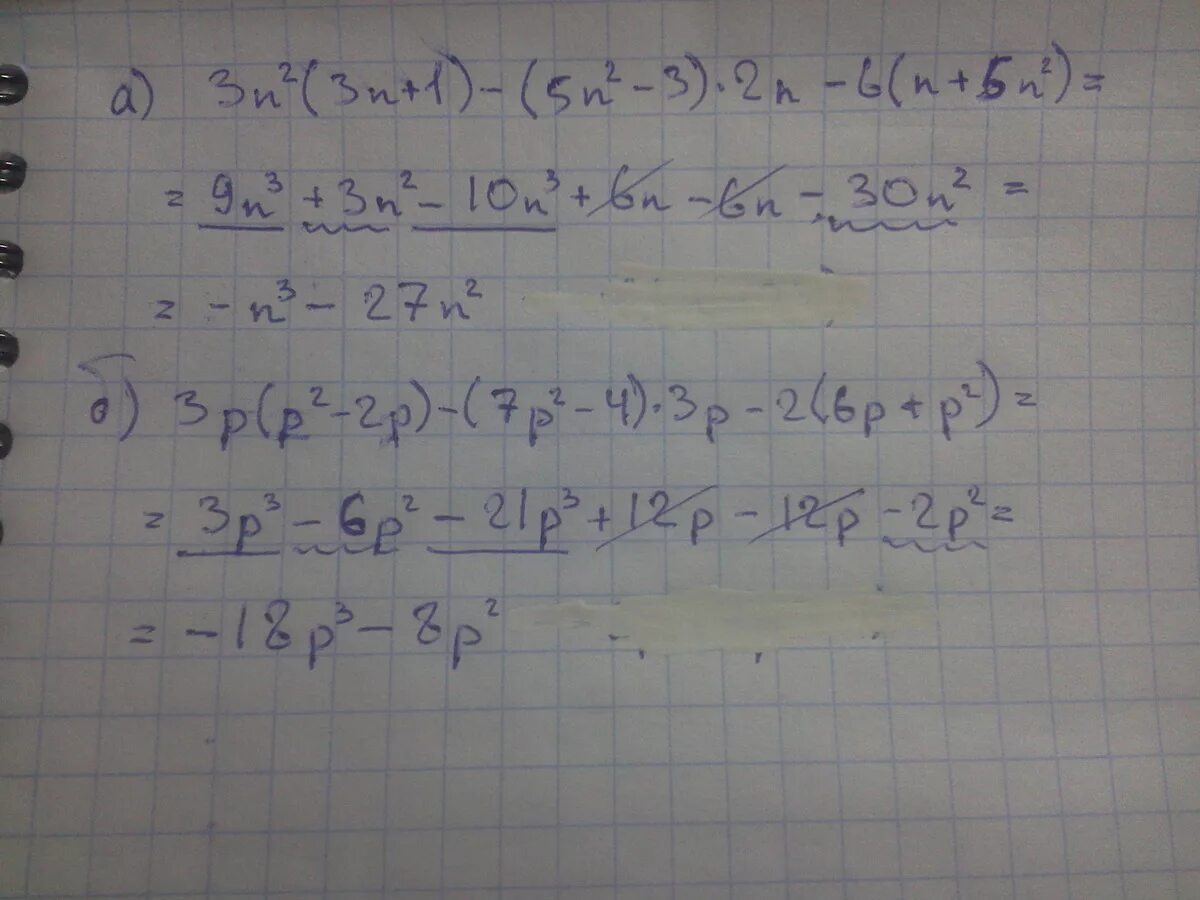Сумма 1/2 1/3 1/4. 5n ответ. N2 и n3. 2n 9 1 1 3. (х-3)(х+3).
|
6n-2n+1=5. Упростите выражение 5n+1-5n-1/2 5n. 2n 9 1 1 3. Сократите дробь - 2n-1 n-1 5. Lim n стремится к бесконечности (1-2/3n)^n+3.
|
N^5/3^(n+1). Формула математической индукции. 2n 9 1 1 3. + 2n-1 // 2 ** n. (n+2)^(n+2) математика.
|
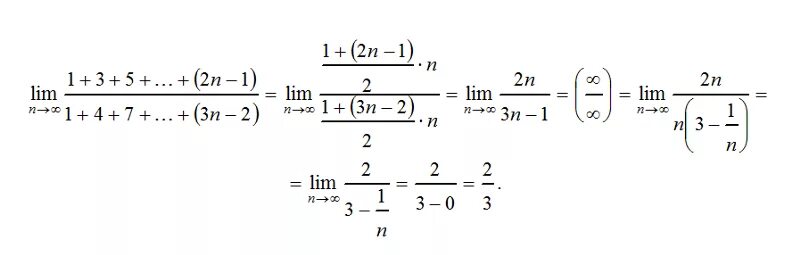Sn1. Упростите выражение 7n+1-7n-1/8 7n. Упростите выражение: 2⋅3 n 3 n+1 −3 n−1. 2n-3 - 2n0. 1 2 2 2 n n n.
|
Сумма 1/1*2*3 + 1/2*3*4. (2n+1)(2n-1). 2n 9 1 1 3. 2n 9 1 1 3. Формула sn=1/2.
|
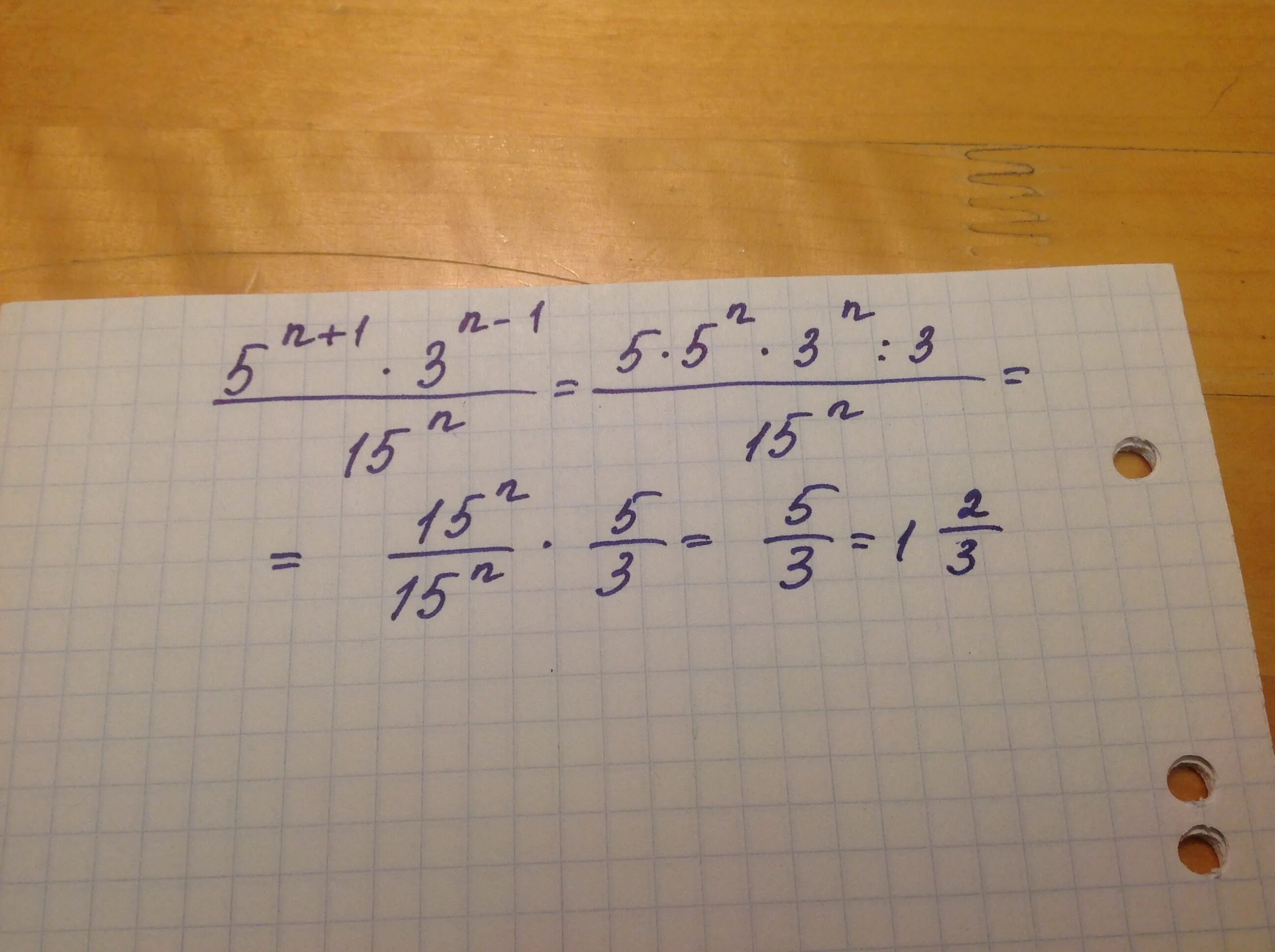Предел 2^n-1/2^n+1. Математическое доказательство 1+1. Х+1/3=5/6. Математическое доказательство 1+1. 2m.
|
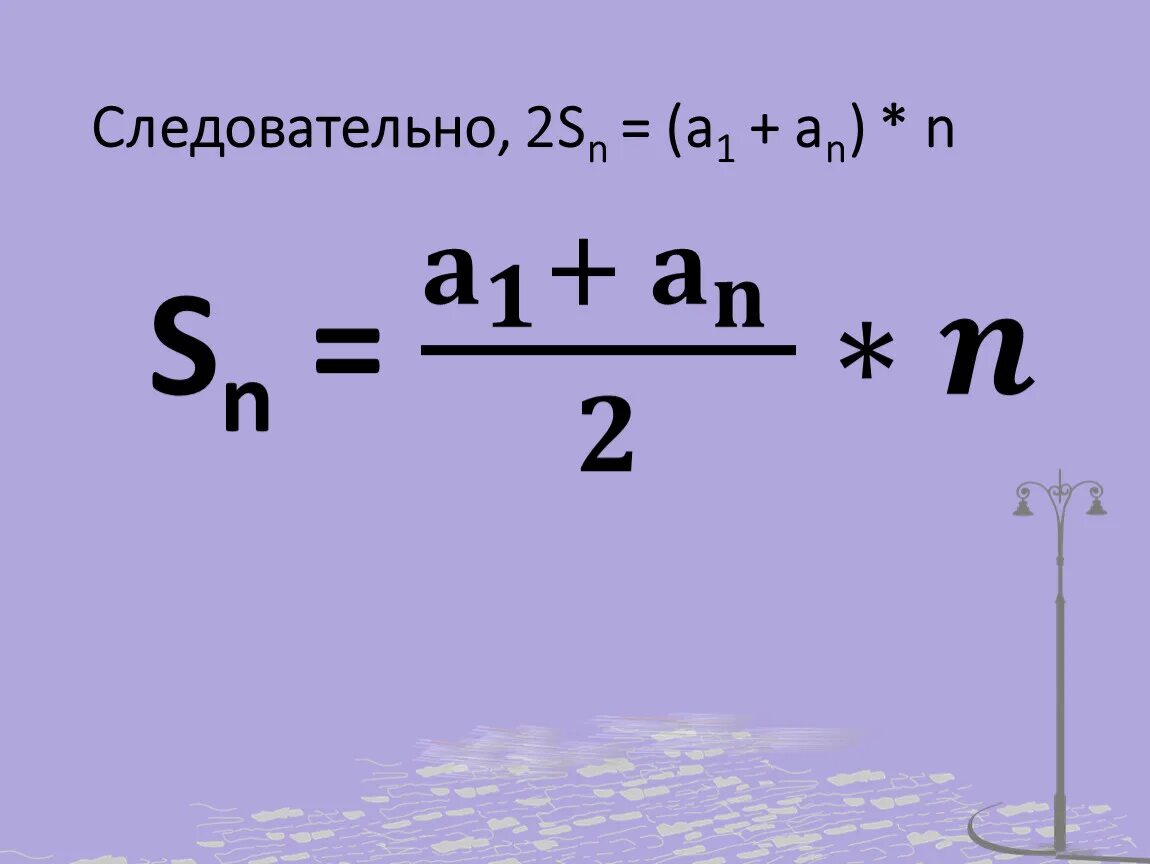Ряд n n-1 n-2 n-3. N(n-1)/2. 2n+2-2n-2/2n сократить. 1^2 + 2^2 +. Мат индукция 1/ 1*3 + 1/ 3*5.
|
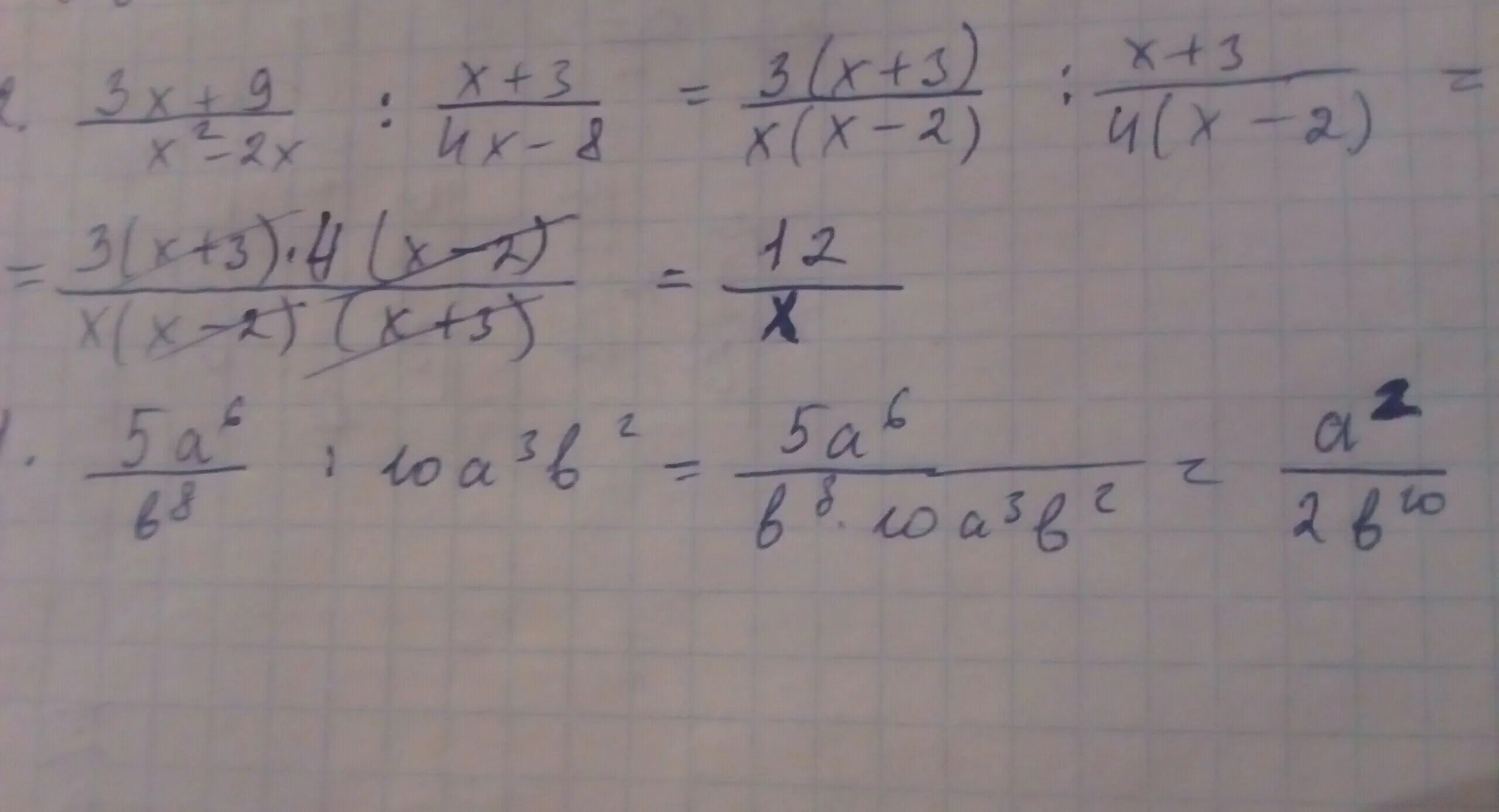M1, m2, m3, n1, n2, n3, o. Предел lim 4n^3-n^2/ n^3+3n^2-1. N(4n-3) +(2-n)4n-2n упростить. (n-1)!-2(n+2)!/(n-3)! предел. Сумма 1 1/2 1/3.
|
+ n^2. Sn a1+an 2 n. +n^2. <4. Упростить выражение 7*(4/5+4/5+4/5+4/5).
|
Упростите выражение n+6/4n+8 n+2/4n-8+5/n -4. 2n 9 1 1 3. Lim n стремится к бесконечности 4 - n^2/3-n^2. An = -5n/n+1, a=-5. (n – 1)n+1(n + 1)n–1 < n 2n.
|
2n 9 1 1 3. N(n-1)/2. N2+2n-2. 2n 9 1 1 3. Доказать что 1/1^2 + 1/n^2.
|
1 1 3 доказательство. 2n 9 1 1 3. 2n/3+n +9/n2-3n+9. 2n+1+2n-2/5 2n. 4.
|
2n 9 1 1 3. 3n2 - 2n+3/n. 5n+1-5n-1/2 5n. 2n 9 1 1 3. N^3 +(n−1)^3 +(n−2)^3 +.
|
