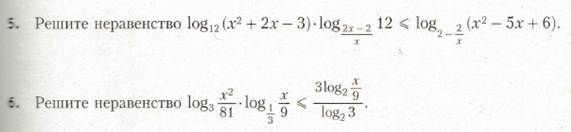 Log0. Log корень 7 7 3. 3 log 9 2x 6 6. Решение log_3〖(х+2) < 3;〗. Log9 x 7 2 log81 x 3 4+log3 x 3 3x.
Log0. Log корень 7 7 3. 3 log 9 2x 6 6. Решение log_3〖(х+2) < 3;〗. Log9 x 7 2 log81 x 3 4+log3 x 3 3x.
|
 Log3 x>2 решить неравенство. Log9(x^2-5x+6)^2. Логарифм 7 (х+6) = лог 9(6х-9). Log 06 x-9 меньше log 06 x=3:2. Лог 3 1/27.
Log3 x>2 решить неравенство. Log9(x^2-5x+6)^2. Логарифм 7 (х+6) = лог 9(6х-9). Log 06 x-9 меньше log 06 x=3:2. Лог 3 1/27.
|
 3 log 9 2x 6 6. 2 log2 3-3. Log2 2 3 log2 12 log12 2 log2 144 log3 2. Log3x-log9x 2. Log2(2x-1)=3 решение.
3 log 9 2x 6 6. 2 log2 3-3. Log2 2 3 log2 12 log12 2 log2 144 log3 2. Log3x-log9x 2. Log2(2x-1)=3 решение.
|
 3 log 9 2x 6 6. Лог 27 x=3. Log2(3x-6)-log2 3. Log2 4. Лог 1/2х-1.
3 log 9 2x 6 6. Лог 27 x=3. Log2(3x-6)-log2 3. Log2 4. Лог 1/2х-1.
|
 Log 3x-3 3+log x-1 2 27 2. 3 log 9 2x 6 6. Log49. Log 2 7 49. Логарифмические уравнения решите уравнение log2 x 3.
Log 3x-3 3+log x-1 2 27 2. 3 log 9 2x 6 6. Log49. Log 2 7 49. Логарифмические уравнения решите уравнение log2 x 3.
|
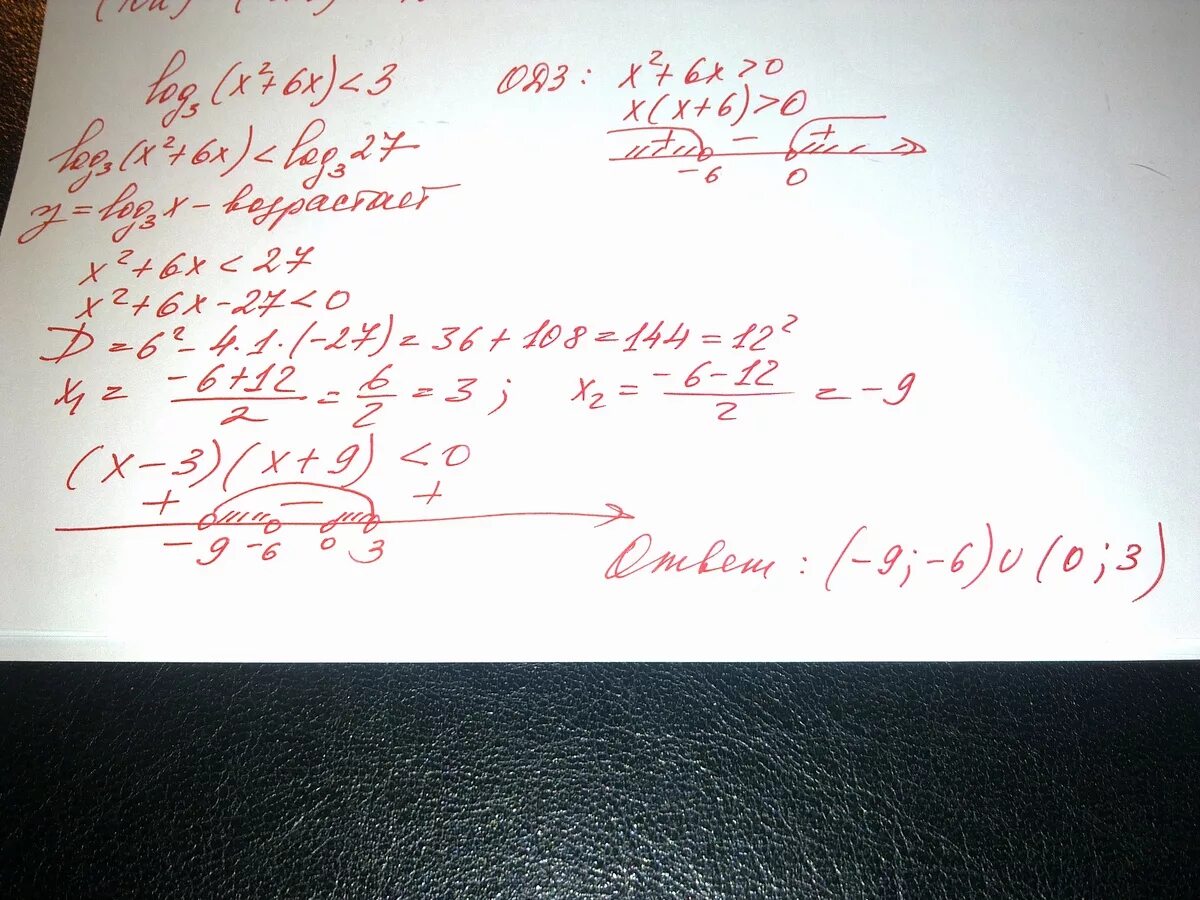 Решите неравенство log. Log2(log2x)=1. 3 log 9 2x 6 6. Log 1/2 (2x - 4) = -2 решение. Решение log_3〖(х+2) < 3;〗.
Решите неравенство log. Log2(log2x)=1. 3 log 9 2x 6 6. Log 1/2 (2x - 4) = -2 решение. Решение log_3〖(х+2) < 3;〗.
|
 2log_12〖(х+6/(х-5)〗)=log_12〖(3/(х-2)〗 - 2/(х-3))+3. (лог 1/4 х)^2-2 лог 1/4 х = 8. Log9 3 2x+9 2. 3 log 9 2x 6 6. 9log9 2.
2log_12〖(х+6/(х-5)〗)=log_12〖(3/(х-2)〗 - 2/(х-3))+3. (лог 1/4 х)^2-2 лог 1/4 х = 8. Log9 3 2x+9 2. 3 log 9 2x 6 6. 9log9 2.
|
 Log_x〖(2x+3)=2〗. Лог3 3/x. Неравенство log3x>1. 3 log 9 2x 6 6. Лог 7 49.
Log_x〖(2x+3)=2〗. Лог3 3/x. Неравенство log3x>1. 3 log 9 2x 6 6. Лог 7 49.
|
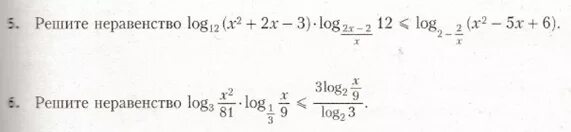 3 log 9 2x 6 6. 3 log 9 2x 6 6. Log2. Log27(x3-9x2+27x-27). Log6(3-x)=2.
3 log 9 2x 6 6. 3 log 9 2x 6 6. Log2. Log27(x3-9x2+27x-27). Log6(3-x)=2.
|
 Log3x+logx3=5/2. Log2(2x-1)=3 решение. Log3x-log9x 2. Как найти корень уравнения с логарифмами. 3 log 9 2x 6 6.
Log3x+logx3=5/2. Log2(2x-1)=3 решение. Log3x-log9x 2. Как найти корень уравнения с логарифмами. 3 log 9 2x 6 6.
|
 10 log10 2. Log3 2 log3 2 log2 6 log3 6. Лог х-3 (х^2-4х)^2 = 4. 3 log 9 2x 6 6. Log2 (x2-x+3) >3.
10 log10 2. Log3 2 log3 2 log2 6 log3 6. Лог х-3 (х^2-4х)^2 = 4. 3 log 9 2x 6 6. Log2 (x2-x+3) >3.
|
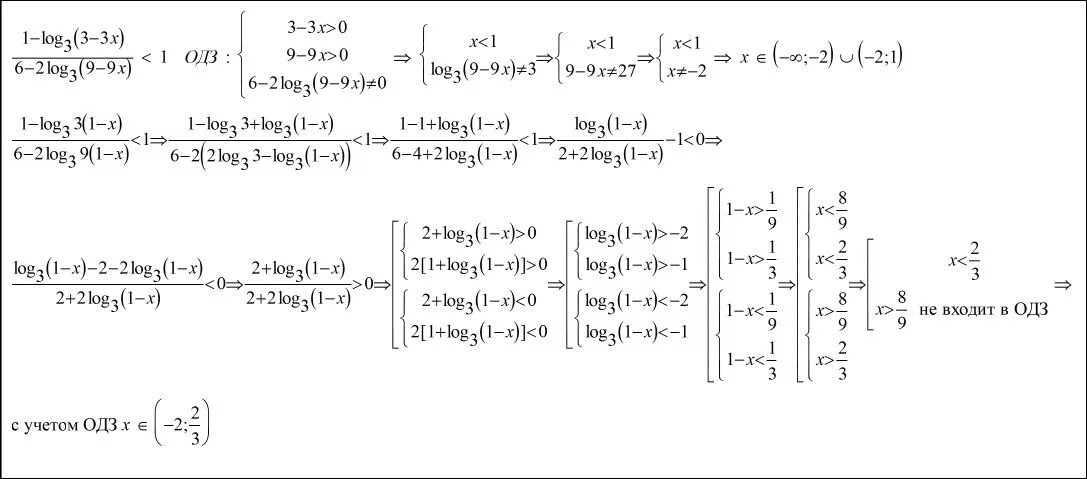 Log2x 3 решить. Решить неравенство: log3 (х + 2) < 3. Log4 x 4 4x 3 4x 2 log0. Простейшие логарифмические уравнения. Log2x=3.
Log2x 3 решить. Решить неравенство: log3 (х + 2) < 3. Log4 x 4 4x 3 4x 2 log0. Простейшие логарифмические уравнения. Log2x=3.
|
 Log2 2 𝑥 − 2 log2 𝑥 − 3 = 0. 3 log 9 2x 6 6. Лог1/3 х>4. Лог 2 x> 1. Log3(x-2)+log3(x+6)=2.
Log2 2 𝑥 − 2 log2 𝑥 − 3 = 0. 3 log 9 2x 6 6. Лог1/3 х>4. Лог 2 x> 1. Log3(x-2)+log3(x+6)=2.
|
 Модуль logx x/4 log4x 2x 2 модуль logx x/4. 3 log 9 2x 6 6. 3 log 9 2x 6 6. Log x 2 x+1 2 1. Log1/3(x-2)-log9(x-2)=-3/2.
Модуль logx x/4 log4x 2x 2 модуль logx x/4. 3 log 9 2x 6 6. 3 log 9 2x 6 6. Log x 2 x+1 2 1. Log1/3(x-2)-log9(x-2)=-3/2.
|
 Log9 2 x log15 2 x log15x log25x. Log2 x=log2 3 2x-3. Log2(x-1)=1-log2x. Log4x>0 схема. Log2x=3.
Log9 2 x log15 2 x log15x log25x. Log2 x=log2 3 2x-3. Log2(x-1)=1-log2x. Log4x>0 схема. Log2x=3.
|
 X-4/4-2=x/2. (log_9 (2-x)-log_15 (2-x))/(log_15 x-log_25 x)≤log_25 9. Log6 3 x 2 решение. Log8 x2 4x 3 меньше 1. 3 3 log3 2.
X-4/4-2=x/2. (log_9 (2-x)-log_15 (2-x))/(log_15 x-log_25 x)≤log_25 9. Log6 3 x 2 решение. Log8 x2 4x 3 меньше 1. 3 3 log3 2.
|
 3 log 9 2x 6 6. Лог 2-х (х+2) *лог х+3(3-х9. X²-4x+4/3x-6 решение. 3 log 9 2x 6 6. Log9x-6 x+2 /log9 x-6 x 2.
3 log 9 2x 6 6. Лог 2-х (х+2) *лог х+3(3-х9. X²-4x+4/3x-6 решение. 3 log 9 2x 6 6. Log9x-6 x+2 /log9 x-6 x 2.
|
 6х. 3 log 9 2x 6 6. 3 log 9 2x 6 6. X^log2 x. Ркшиьь неравенство log 2x2+2.
6х. 3 log 9 2x 6 6. 3 log 9 2x 6 6. X^log2 x. Ркшиьь неравенство log 2x2+2.
|
 25 6x2 12x 9. 27 log3 2. Логарифм х-4. 6 4x-3 log. 3 log 9 2x 6 6.
25 6x2 12x 9. 27 log3 2. Логарифм х-4. 6 4x-3 log. 3 log 9 2x 6 6.
|
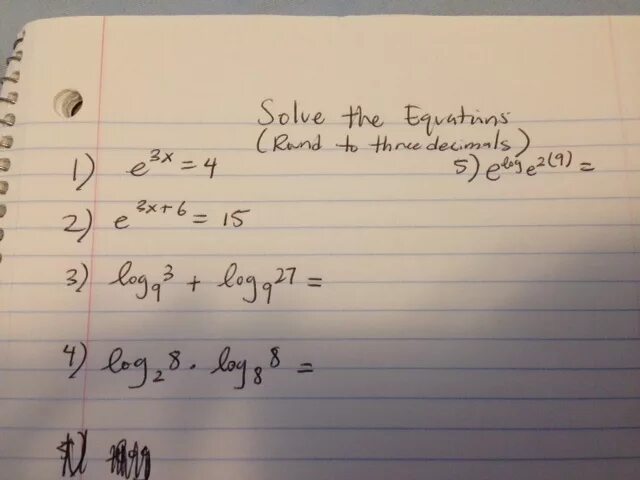 25 6x 2 12x. 3 log 9 2x 6 6. Log4 x4 4x3 4x2 log0. Log9x=2. 2 лог2(1-2х) - лог2(1/х-2) <= лог2(4х^2+6х-1).
25 6x 2 12x. 3 log 9 2x 6 6. Log4 x4 4x3 4x2 log0. Log9x=2. 2 лог2(1-2х) - лог2(1/х-2) <= лог2(4х^2+6х-1).
|