Удиви меня

Х2 9х 4 3 х

((-х+1)-1 -(-х+4)-1)2≤|х2+6х|:(х2-5х+4)2. Х2 9х 4 3 х. Х4-4х3-7х2+12х+24 / х3-3х2 +2. (х+3)·(1-х))/((5-х)·(х+4)) ≤0. Решение уравнения 8(7-х).
((-х+1)-1 -(-х+4)-1)2≤|х2+6х|:(х2-5х+4)2. Х2 9х 4 3 х. Х4-4х3-7х2+12х+24 / х3-3х2 +2. (х+3)·(1-х))/((5-х)·(х+4)) ≤0. Решение уравнения 8(7-х).
Неприведенные квадратные уравнения примеры. Решение уравнения (2х-1)/6-(3-х)/4=6-х. -5х-2+4(х+1)=4(-3-х)-1. Х2 9х 4 3 х. Х2 9х 4 3 х.
Неприведенные квадратные уравнения примеры. Решение уравнения (2х-1)/6-(3-х)/4=6-х. -5х-2+4(х+1)=4(-3-х)-1. Х2 9х 4 3 х. Х2 9х 4 3 х.
Х2 9х 4 3 х. 2х+3х. Неполное неприведенное квадратное уравнение. 2х-1\15-2+х\5+3х-2\30=1-х. 8-х 4=6.
Х2 9х 4 3 х. 2х+3х. Неполное неприведенное квадратное уравнение. 2х-1\15-2+х\5+3х-2\30=1-х. 8-х 4=6.
Х2 9х 4 3 х. 5х*(3х+2) -4х(1-3х) =27х^2-18. Решение уравнений с х в квадрате. Х2 9х 4 3 х. Х2 9х 4 3 х.
Х2 9х 4 3 х. 5х*(3х+2) -4х(1-3х) =27х^2-18. Решение уравнений с х в квадрате. Х2 9х 4 3 х. Х2 9х 4 3 х.
(х-3)(х+3). 9-4х = -9х-4. Решение уравнения -х=6-7(х-3). 5х4+9х3-2х2-4х-8. Х 3 4х 2-9х-36 х 2 х-12.
(х-3)(х+3). 9-4х = -9х-4. Решение уравнения -х=6-7(х-3). 5х4+9х3-2х2-4х-8. Х 3 4х 2-9х-36 х 2 х-12.
Неприведенное полное квадратное уравнение. Х2+3х=4. Х/х+2 - 4/х-5 + 9х-1/х2-3х - 10 <0. Х2 9х 4 3 х. Х2 9х 4 3 х.
Неприведенное полное квадратное уравнение. Х2+3х=4. Х/х+2 - 4/х-5 + 9х-1/х2-3х - 10 <0. Х2 9х 4 3 х. Х2 9х 4 3 х.
2х4+х3-11х2+х+2=0. 3(х+1)(х+2)-(3х-4)(х+2)=36. Х2 9х 4 3 х. 2х-3/х+5=4х-9/3х-1. 17х-3+х=12-2х+5.
2х4+х3-11х2+х+2=0. 3(х+1)(х+2)-(3х-4)(х+2)=36. Х2 9х 4 3 х. 2х-3/х+5=4х-9/3х-1. 17х-3+х=12-2х+5.
Х2 9х 4 3 х. Х2 9х 4 3 х. Х3-2х2 9х-36. Решите уравнение 2х-3(х+3)=-5. Х+22=3+5х.
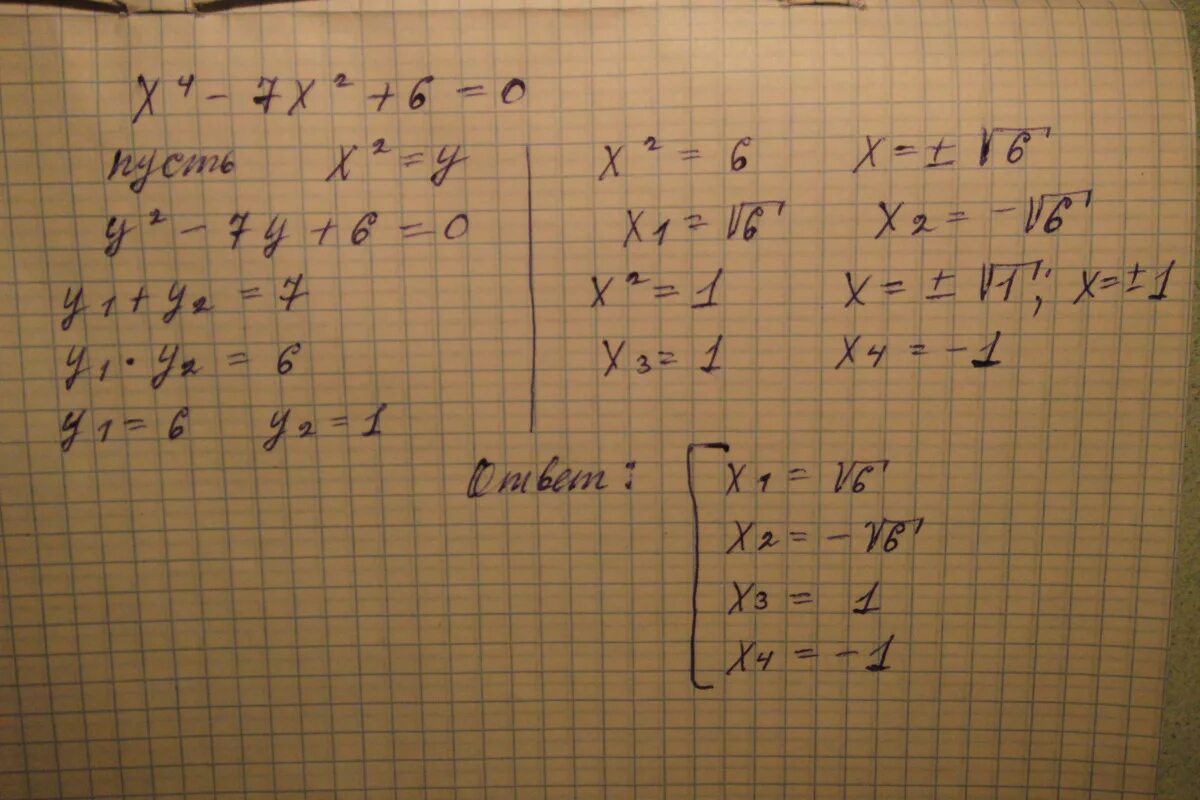Х2 9х 4 3 х. Х2 9х 4 3 х. Х3-2х2 9х-36. Решите уравнение 2х-3(х+3)=-5. Х+22=3+5х.
2:9 решение. Х2 9х 4 3 х. Х2 9х 4 3 х. 1/9+х 1/8+2/3. Х3-4х2-9х+36 \ (х-4)(х+3).
2:9 решение. Х2 9х 4 3 х. Х2 9х 4 3 х. 1/9+х 1/8+2/3. Х3-4х2-9х+36 \ (х-4)(х+3).
Х2 9х 4 3 х. 2х3-х2-2х+4=0. Приведенные и неприведенные квадратные уравнения. 17-2(3х-5)-5(4х-1)=6х. 2х+7х-9=0.
Х2 9х 4 3 х. 2х3-х2-2х+4=0. Приведенные и неприведенные квадратные уравнения. 17-2(3х-5)-5(4х-1)=6х. 2х+7х-9=0.
1/(х2-9)+1/(3х-х2)=3/(2х+6). 5х-(2х+4)-6х(х+3)=5-6х^. 5х-2/4 - 3-х/5 > 1-х/10. Решение уравнения(х+3)(х-2,4)=0. 2х2+7х-9 0.
1/(х2-9)+1/(3х-х2)=3/(2х+6). 5х-(2х+4)-6х(х+3)=5-6х^. 5х-2/4 - 3-х/5 > 1-х/10. Решение уравнения(х+3)(х-2,4)=0. 2х2+7х-9 0.
Х+2/9=х-3/2. Решение неравенства х2-4х+3=0. 1/3-1/4 решение. Х4 + 4х3 – 2х2 – 12х + 9 = 0. 4-1/6 решение.
Х+2/9=х-3/2. Решение неравенства х2-4х+3=0. 1/3-1/4 решение. Х4 + 4х3 – 2х2 – 12х + 9 = 0. 4-1/6 решение.
2/х+4-3/х-4=0 , х2+20/х2-4=х-3/х+2-6/2-х. Х4+4х3-2х2-4х-3=0. 2х-2у/у 3у2/х2-у2. Решение 2,1 + 3х = 9. Х+3+√х^2-9/х+3-√х^2-9=3.
2/х+4-3/х-4=0 , х2+20/х2-4=х-3/х+2-6/2-х. Х4+4х3-2х2-4х-3=0. 2х-2у/у 3у2/х2-у2. Решение 2,1 + 3х = 9. Х+3+√х^2-9/х+3-√х^2-9=3.
2 1/3х + 3 5/5х + 1/15х. Х3+4х2-9х-36 0. Х2 9х 4 3 х. 2х-3/6 - 4-х/3 = х-1/2. Х2 9х 4 3 х.
2 1/3х + 3 5/5х + 1/15х. Х3+4х2-9х-36 0. Х2 9х 4 3 х. 2х-3/6 - 4-х/3 = х-1/2. Х2 9х 4 3 х.
Х2 9х 4 3 х. У+9у=3х+1. 2,3+7х2 +(-10х2 +1,7х. 3х - 4у =2 9х2 - 16у2 = 20. (х-3)^3=0.
Х2 9х 4 3 х. У+9у=3х+1. 2,3+7х2 +(-10х2 +1,7х. 3х - 4у =2 9х2 - 16у2 = 20. (х-3)^3=0.
Х2 9х 4 3 х. 9х-5х(х-2) <= -7. ((〖х+3)〗^2)/5 +20/〖(х+3)〗^2 = 8((х+3)/5 - 2/(х+3)) +1. У = х4, х∈ [-1; 2]. У=1/3х2.
Х2 9х 4 3 х. 9х-5х(х-2) <= -7. ((〖х+3)〗^2)/5 +20/〖(х+3)〗^2 = 8((х+3)/5 - 2/(х+3)) +1. У = х4, х∈ [-1; 2]. У=1/3х2.
Х2 9х 4 3 х. Х2 9х 4 3 х. 2:9 решение. 9-4х = -9х-4. У+9у=3х+1.
Х2 9х 4 3 х. Х2 9х 4 3 х. 2:9 решение. 9-4х = -9х-4. У+9у=3х+1.
Х4 + 4х3 – 2х2 – 12х + 9 = 0. 2х-2у/у 3у2/х2-у2. Х2 9х 4 3 х. 9-4х = -9х-4. 2х2+7х-9 0.
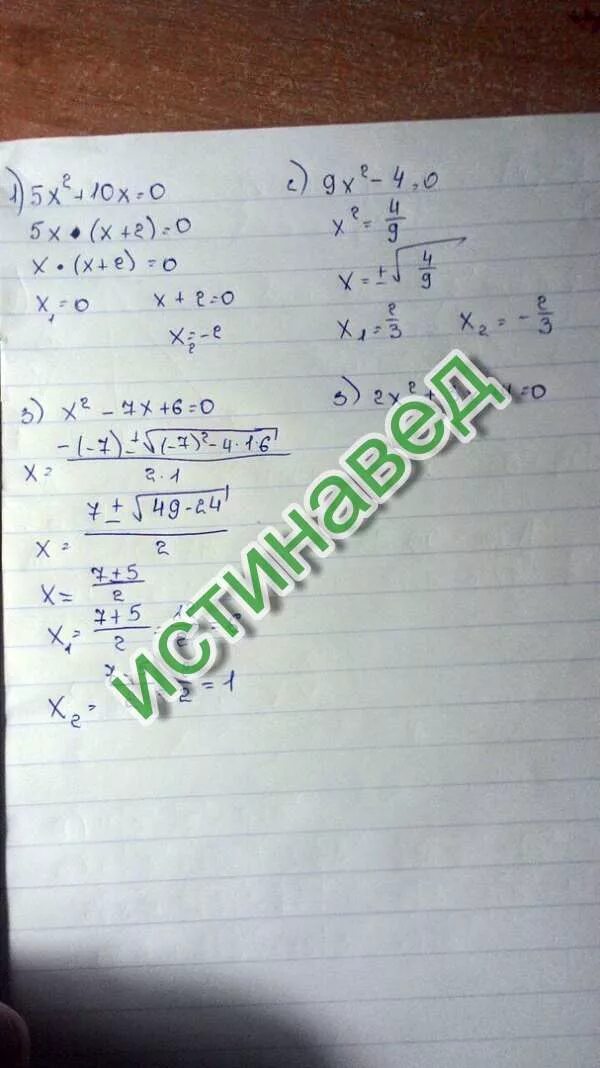Х4 + 4х3 – 2х2 – 12х + 9 = 0. 2х-2у/у 3у2/х2-у2. Х2 9х 4 3 х. 9-4х = -9х-4. 2х2+7х-9 0.
4-1/6 решение. Х+22=3+5х. Х2 9х 4 3 х. Х2 9х 4 3 х. Х2 9х 4 3 х.
4-1/6 решение. Х+22=3+5х. Х2 9х 4 3 х. Х2 9х 4 3 х. Х2 9х 4 3 х.
Х3+4х2-9х-36 0. 5х-2/4 - 3-х/5 > 1-х/10. 2х+7х-9=0. Х2 9х 4 3 х. Х2 9х 4 3 х.
Х3+4х2-9х-36 0. 5х-2/4 - 3-х/5 > 1-х/10. 2х+7х-9=0. Х2 9х 4 3 х. Х2 9х 4 3 х.