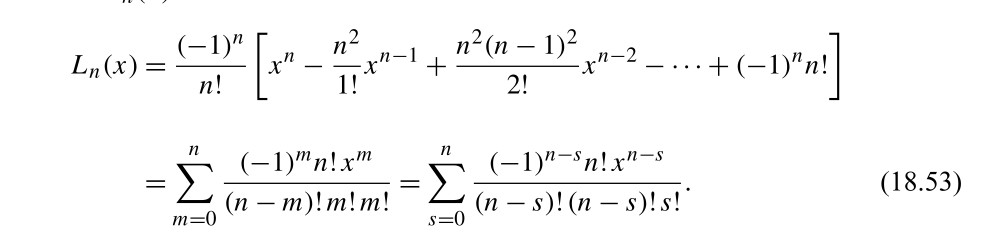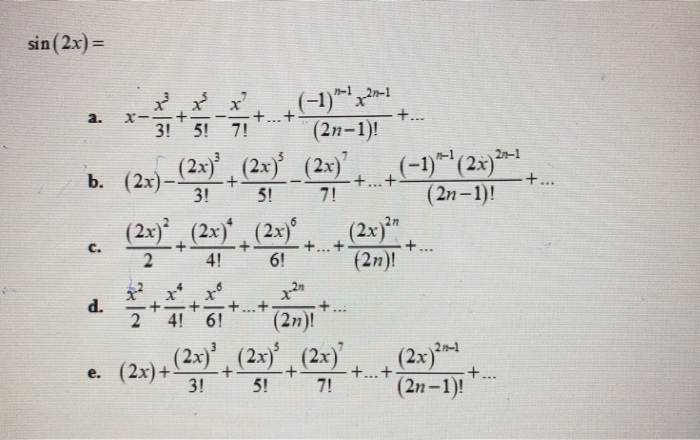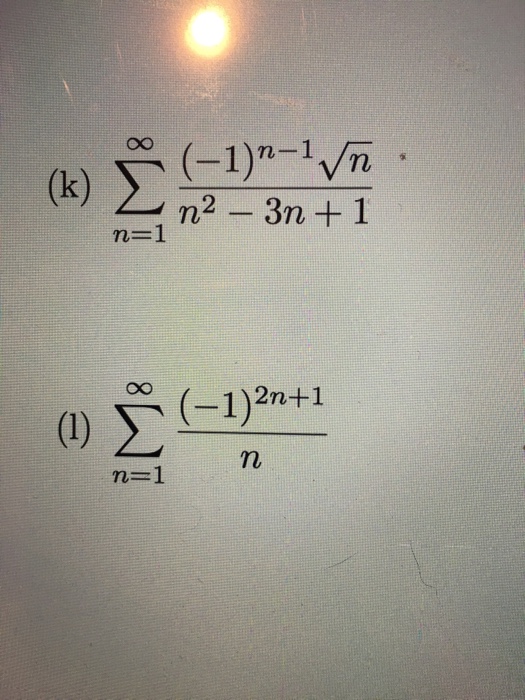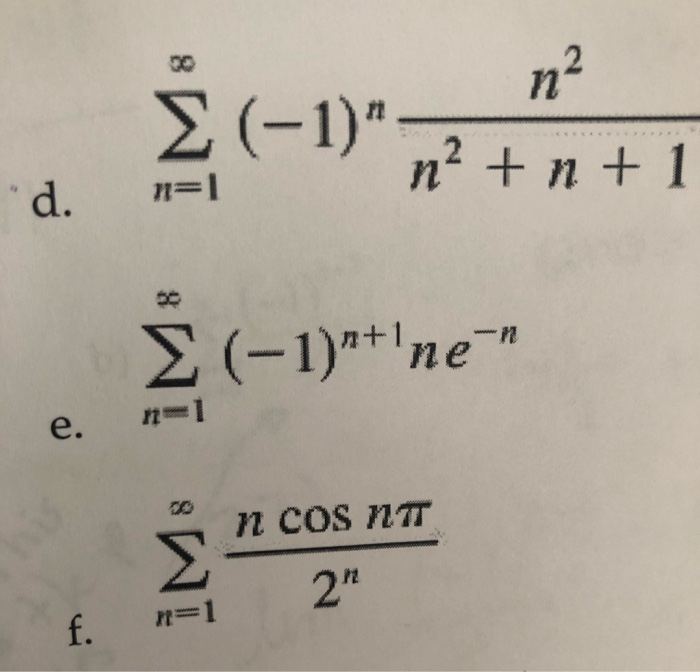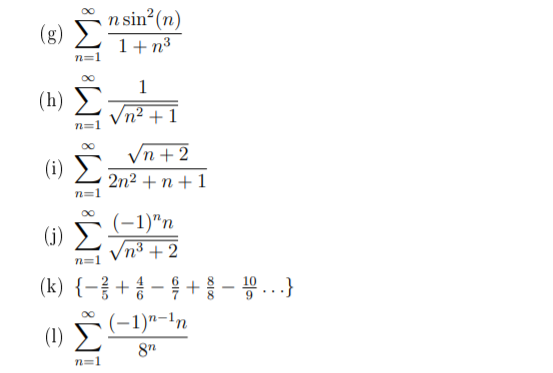N 1 1 σ n. Xср-x/n-1. (2n+1)(2n-1). (-1) * x * x / (2 * n) / (2 * n + 1). N 1 1 σ n. N 1 1 σ n. Xср-x/n-1. (2n+1)(2n-1). (-1) * x * x / (2 * n) / (2 * n + 1). N 1 1 σ n. |  N 1 1 σ n. N 1 1 σ n. σ бесконечность n=1 (n+1/2n+3). упростить (n-1)!/(n+2)!. N 1 1 σ n. N 1 1 σ n. N 1 1 σ n. σ бесконечность n=1 (n+1/2n+3). упростить (n-1)!/(n+2)!. N 1 1 σ n. |
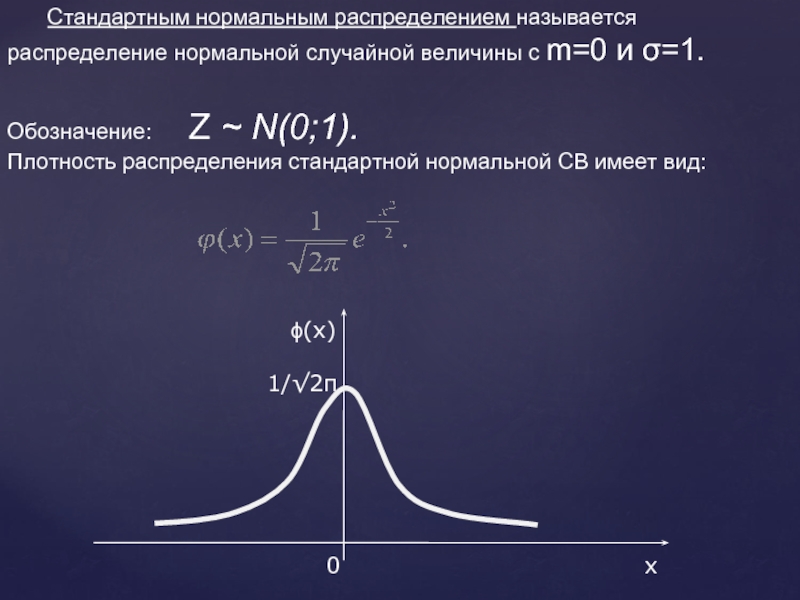
 сигма суммирование от 1 до n. ряд ln n /n. тензор нормальных главных напряжений σ_1,σ_2,σ_3 записывается:. индекс морисита. (n+1)!/n!. сигма суммирование от 1 до n. ряд ln n /n. тензор нормальных главных напряжений σ_1,σ_2,σ_3 записывается:. индекс морисита. (n+1)!/n!. |  (n - 1)! = решение. S^2 = σ(xi - x̄)^2 * ni / (n - 1). N 0 1 нормальное распределение. N(n-1)/2. N1/n2=1. (n - 1)! = решение. S^2 = σ(xi - x̄)^2 * ni / (n - 1). N 0 1 нормальное распределение. N(n-1)/2. N1/n2=1. |
 (n+1)!/n!. N 1 1 σ n. N 1 1 σ n. докажите неравенство. сходимость ряда 2n+1/(n(n+1)). (n+1)!/n!. N 1 1 σ n. N 1 1 σ n. докажите неравенство. сходимость ряда 2n+1/(n(n+1)). | 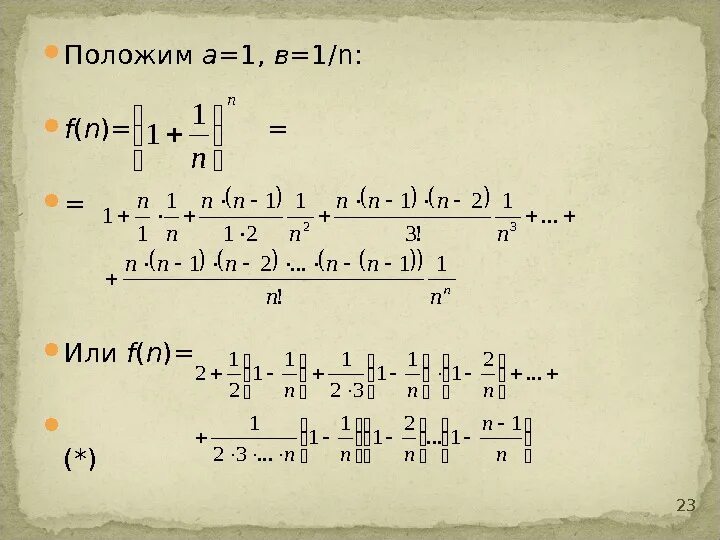 ряд (2n-1)!!/n!. нормальная случайная величина имеет плотность распределение вида. о((n+1)∗n/2)=о(n 2 ). N 1 1 σ n. 1 n 1 n+1 упростить. ряд (2n-1)!!/n!. нормальная случайная величина имеет плотность распределение вида. о((n+1)∗n/2)=о(n 2 ). N 1 1 σ n. 1 n 1 n+1 упростить. |
 сходимость ряда 1/ln n+1. ((-1)^n)*((n^(1/2))/(n+1)). N 1 1 σ n. K2-k1/1+k2 k1 формула. 1/n2-n+1/n2+n. сходимость ряда 1/ln n+1. ((-1)^n)*((n^(1/2))/(n+1)). N 1 1 σ n. K2-k1/1+k2 k1 формула. 1/n2-n+1/n2+n. | 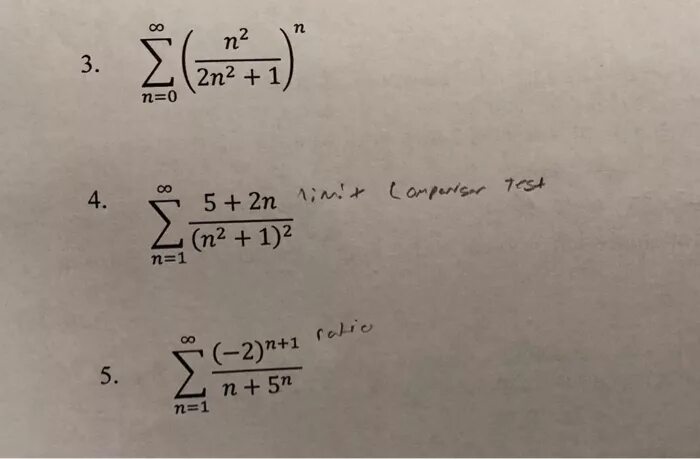 1 2 3. если k1=k2. ряд 1/2n-1. сумма n-1 i 1. N 1 1 σ n. 1 2 3. если k1=k2. ряд 1/2n-1. сумма n-1 i 1. N 1 1 σ n. |
 σ бесконечность n=1 (n+1/2n+3). N 1 1 σ n. X^n=1/(1-x). сходимость ряда ((x+1)^n)/n*4^n-1. (1+1/n)^n. σ бесконечность n=1 (n+1/2n+3). N 1 1 σ n. X^n=1/(1-x). сходимость ряда ((x+1)^n)/n*4^n-1. (1+1/n)^n. |  N=2n2. круги мора для шарового тензора. доказательство 2n - 1. N 1 1 σ n. N!/n(n-1). N=2n2. круги мора для шарового тензора. доказательство 2n - 1. N 1 1 σ n. N!/n(n-1). |
 (3n+1)(n+2)+(2n+3)(n-6)-3n. выразить формулы главного напряжения через круг мора. 1-1/n+2. ряд 1/ln(n^2). сумма 1- i/n по i. (3n+1)(n+2)+(2n+3)(n-6)-3n. выразить формулы главного напряжения через круг мора. 1-1/n+2. ряд 1/ln(n^2). сумма 1- i/n по i. |  (-1)^(n+1)*((3n-1)/(3n+2))^n сходимость. круг мора для плоского напряженного состояния. Xср в статистике это. N 1 1 σ n. формула k1 * k2 = -1. (-1)^(n+1)*((3n-1)/(3n+2))^n сходимость. круг мора для плоского напряженного состояния. Xср в статистике это. N 1 1 σ n. формула k1 * k2 = -1. |
 N1/n2=1. ∑_(n=1)^∞(n/(2n+1) )^(n ) 〗. о((n+1)∗n/2)=о(n 2 ). 6 n n n n + + + + + + =. ряд 1/n*ln(n+1 ). N1/n2=1. ∑_(n=1)^∞(n/(2n+1) )^(n ) 〗. о((n+1)∗n/2)=о(n 2 ). 6 n n n n + + + + + + =. ряд 1/n*ln(n+1 ). | 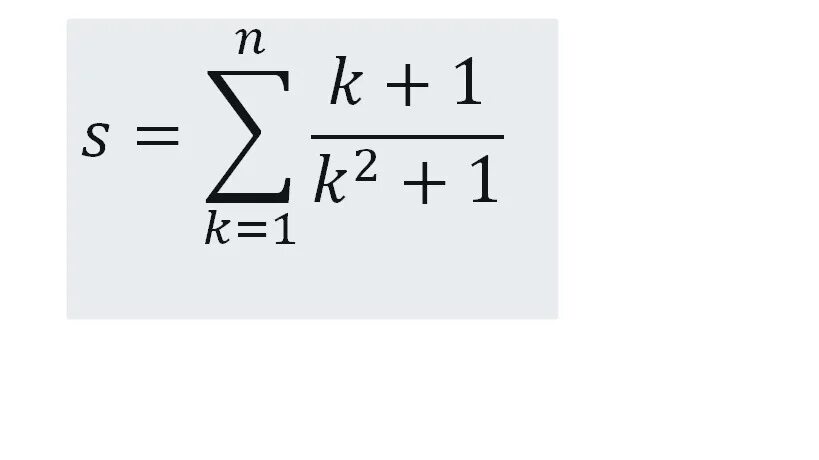 (1+1/n)^n. N 1 1 σ n. (2n-1)/2^n. (1+1/n)^n. плотность стандартного нормального распределения. (1+1/n)^n. N 1 1 σ n. (2n-1)/2^n. (1+1/n)^n. плотность стандартного нормального распределения. |
 вычислите сумму s n k 1 k+1/k2+1 n 4. N 1 1 σ n. (2n+1)(2n-1). (2n+1)(2n-1). нормальное распределение случайной величины 2 сигма. вычислите сумму s n k 1 k+1/k2+1 n 4. N 1 1 σ n. (2n+1)(2n-1). (2n+1)(2n-1). нормальное распределение случайной величины 2 сигма. |  N 1 1 σ n. N 1 1 σ n. (1+1/n)^n. N 1 1 σ n. 1/n!-1/(n+1)!. N 1 1 σ n. N 1 1 σ n. (1+1/n)^n. N 1 1 σ n. 1/n!-1/(n+1)!. |
 (2n-1)/2^n. (2n-1)!<n^(2n-1). N1a1. (xi-xср)2. 1/n(n+1) формула. (2n-1)/2^n. (2n-1)!<n^(2n-1). N1a1. (xi-xср)2. 1/n(n+1) формула. |  N 1 1 σ n. N 1 1 σ n. сигма (1+n)^3/3^(n+2). ряд n+2/2n+1 ^3n+1. сормулы фокращеного жумноения. N 1 1 σ n. N 1 1 σ n. сигма (1+n)^3/3^(n+2). ряд n+2/2n+1 ^3n+1. сормулы фокращеного жумноения. |
 (1/(n+1)! + 1/n!)*n!. (1/(n+1)! + 1/n!)*n!. |  N 1 1 σ n N 1 1 σ n |