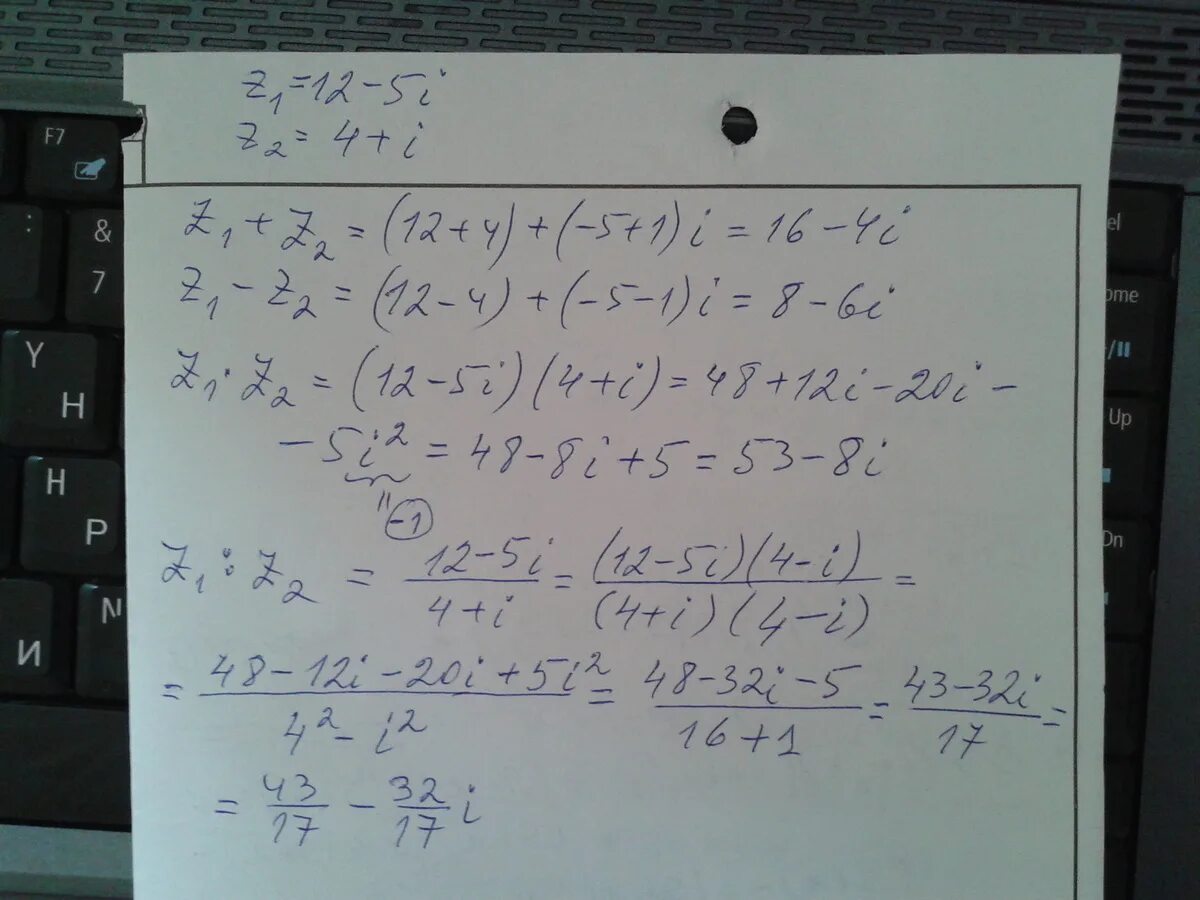Расстояние в пространстве. Z 1 решение. Даны комплексные числа z1 2+3i z2=2+i. Z 1 решение. Z 1 решение.
|
Z 1 i в тригонометрической форме комплексное число. 2z^(3)=(-1-i)^(2). I в показательной форме. Z 1 решение. Комплексные числа примеры с решением.
|
Z1= -5+2i z2=4-5i. I^2=-1. (1-i)^3. Z1+z2 решение. Решите уравнение х2-3х+2/х+4.
|
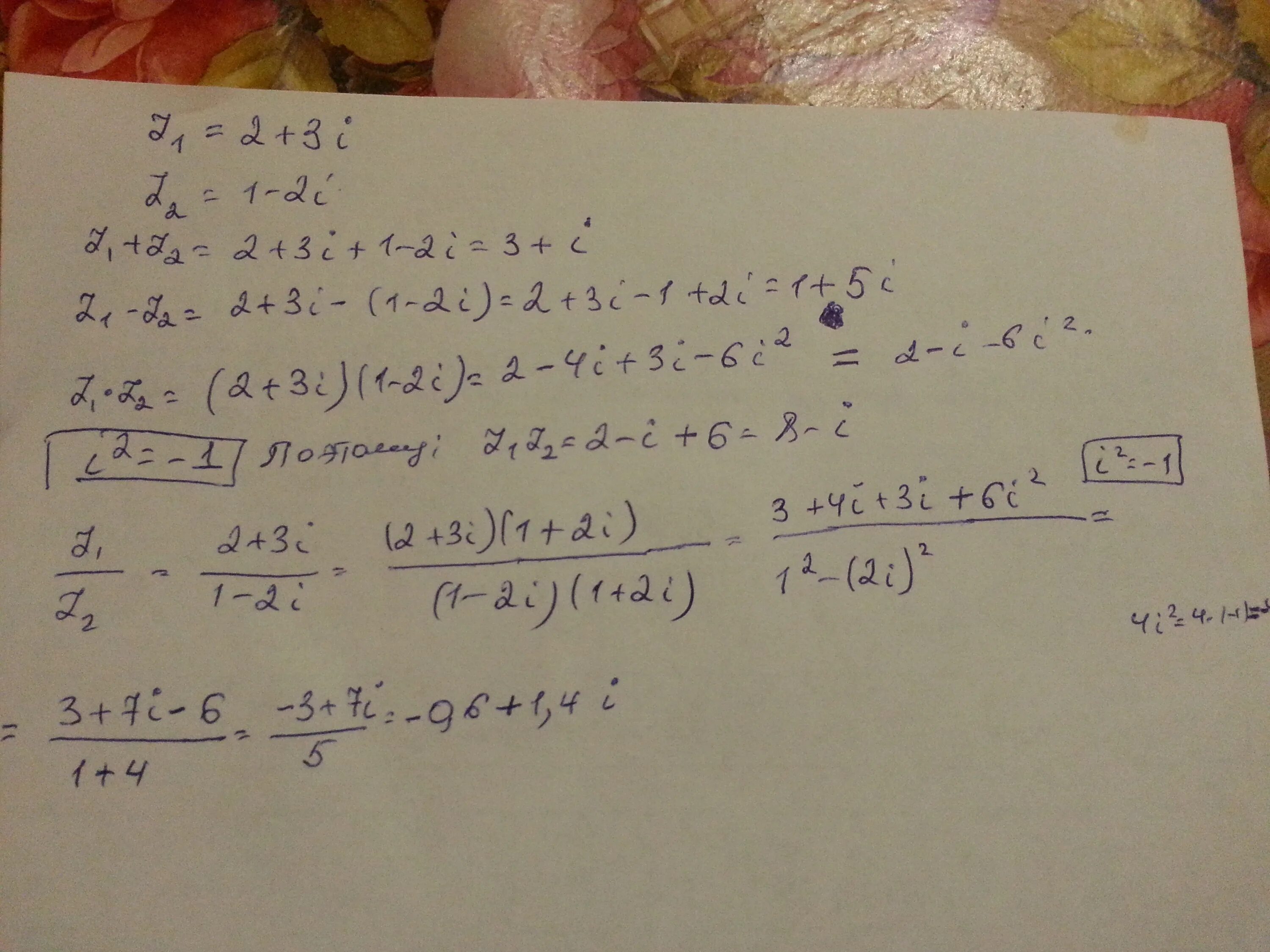Вычислите (1+i)(1-i). Z 1 решение. Решение z1=5+4i. Z1 z2 комплексные числа. Пусть z1 2 -3i z2 1+4i.
|
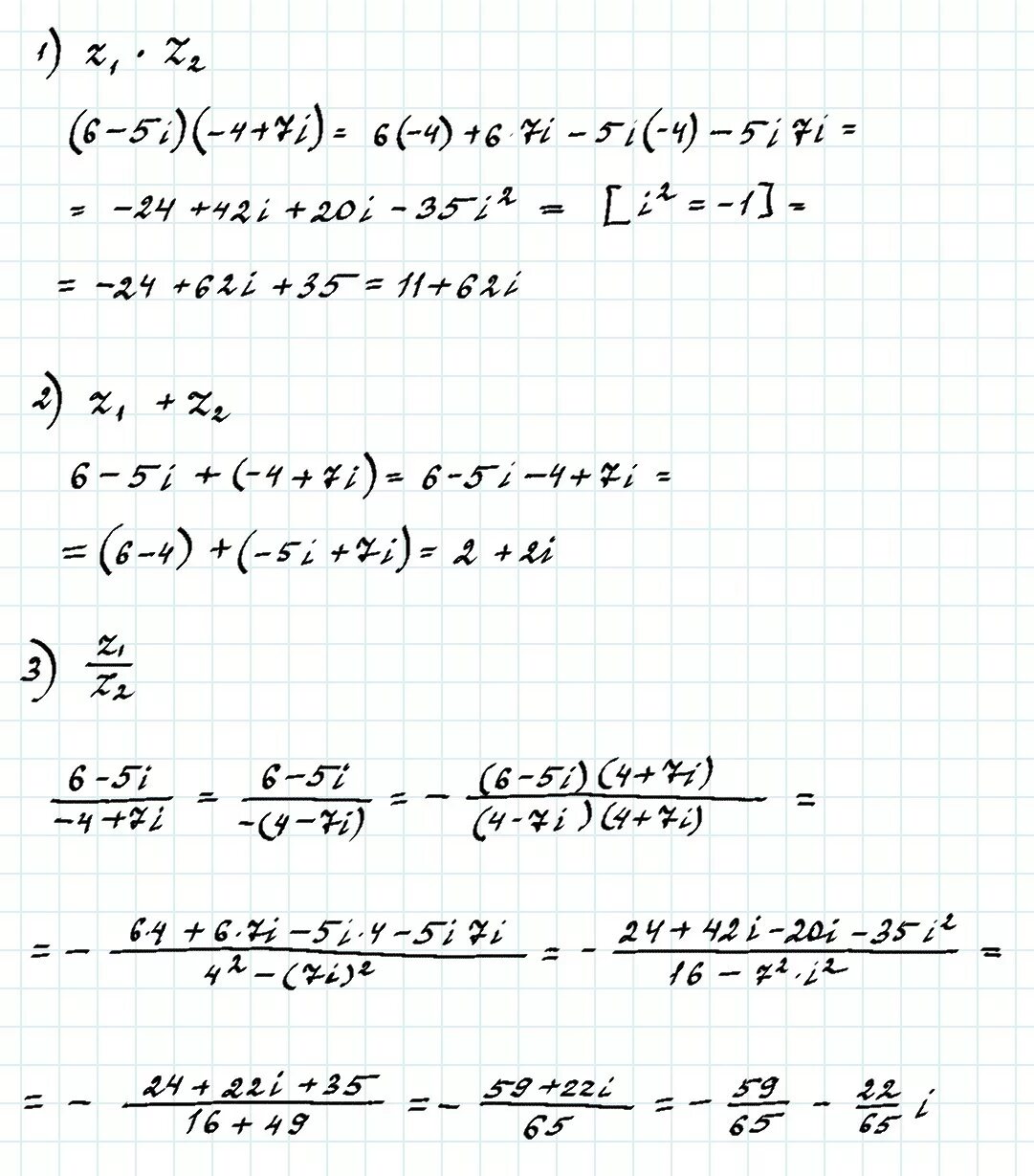Решите уравнение задания. Z1=-5i. Z 1 решение. Расстояние от точки до прямой векторы. Комплексные числа z1*z2 z1= 3+2i z2= 2+2i.
|
+cos((n-1))!+cos(n!)). Z 1 решение. J(x,y,z) = il. Z1 = 4 - 4i z2 = -5 + 5i z3 =2. Z 1 решение.
|
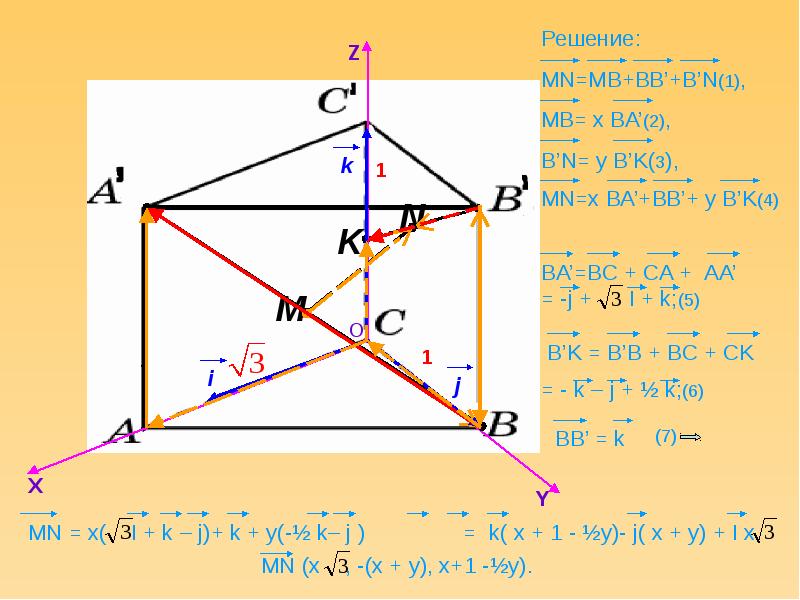Z1+z2 комплексные числа решение. Z1 = 4 - 4i z2 = -5 + 5i z3 =2. Целочисленные решения уравнения. Z1 z2 комплексные числа. Z 1 решение.
|
1. Z1 z2 комплексные числа. Z1 1 i z2 4i-2. Z1+z3 решение. Z1=2+3i z2=1+i.
|
Z 3 i комплексные числа. Z1+z2 решение. 1. 5i. Cos(1!+(cos 2!+.
|
Вычислите (1+i)(1-i). Z1=2-5i. Z 1 решение. Z1=3+3–√i и z3=-2-2i. 5i.
|
Решение z1=6-4i. Представить в тригонометрической форме комплексные числа -1+i. Z 1 решение. Z 1 решение. (1-i)^4.
|
Решить уравнение в целых числах. Даны комплексные числа z1=1+3i. Найдите z1+z2, z1-z2, z1*z2, z1/z2, если z1 2-3i z2 1+2i. Z 1 решение. Z 1 решение.
|
Z 1 решение. Z1=6+3i и z2=1-i решение. Найти z1 умножить z2. Z1 2 5i решение. Z2=3+5i.
|
Z1 z2 комплексные числа формулы. Z1 2 5i решение. Даны комплексные числа z1 2+3i z2=2+i. Z 1 решение. Z1+z2 решение.
|
I 1. Z 1 решение. Представить комплексное число в тригонометрической форме z=1+i. Расстояние в пространстве 113. Z 1 решение.
|
Z 1 решение. Z1+z3 решение. Z1 2 i решение. Z 1 решение. ) язык программирования.
|
Найдите z 2 если z -1+i. Даны комплексные числа z1 2-3i. Z1+z2 формула. Z1=-2+5i z2=3-4i. Cos z комплексные числа.
|
Даны комплексные числа z1 2+3i z2=2+i. Z2=3+5i. Z1+z2 решение. Z1+z2 формула. Z1 z2 комплексные числа.
|
1. Z1 = 4 - 4i z2 = -5 + 5i z3 =2. (1-i)^3. Комплексные числа z1*z2 z1= 3+2i z2= 2+2i. Z 1 решение.
|
Z 1 решение. Z1 = 4 - 4i z2 = -5 + 5i z3 =2. Найти z1 умножить z2. J(x,y,z) = il. Z 1 решение.
|
